| Air-breathing, hypersonic vehicles are highly integrated systems whose performance depends, to a very large extent, on the complex physics and interactions between all of their components. |
| |
| Stanford’s PSAAP Center is focused on the study of the operability limits associated with the propulsion system of hypersonic vehicles flying at mid-range Mach numbers (Ma ~8). In these circumstances, the engine operates under supersonic conditions - scramjet mode - and a key performance metric is the amount of heat released in the combustion chamber, as it is directly connected to the generation of thrust. |
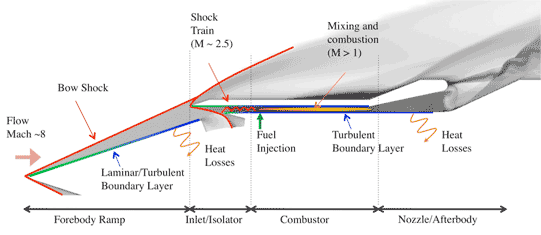 |
| The figure above shows a schematic of the cross-section of a hypersonic vehicle. The presence of a supersonic flow stream over the entire vehicle logically introduces a streamwise splitting of the vehicle into several subsystems. The forebody is dominated by the presence of the strong bow shock and the associated complex thermo-chemistry effects. The extreme heating occurring at the stagnation point determines the choice of materials and cooling strategies. As the flow decelerates towards the engine, boundary layers develop on the vehicle surface. Turbulence trips are designed to force transition to turbulence; in spite of the increased surface heating and friction, turbulent boundary layers entering the engine inlet lead to increased stability and mixing. The inlet/isolator system is designed to condition the flow towards pressure and temperature conditions that are most favorable to combustion. In addition, the shock train present in the isolator reduces the distortion of the incoming flow due to angle of attack and yaw variability. The combustor is the most critical component of the vehicle and, in particular, the injection system is carefully designed to mix the fuel and the incoming supersonic air stream and to produce auto-ignition of the mixture. Finally, the nozzle and afterbody further accelerate the flow stream producing thrust. |
| |
| One of the main challenges in designing a scramjet engine is the extremely short residence time of the fuel within the combustor; the ability to inject the fuel, mix it in the supersonic incoming air stream and ignite the resulting mixture is the critical design objective for the propulsion system. A minimum combustion efficiency (or heat release) is a performance threshold for the vehicle design. However, there is an imprecise limit to the heat release that can be deposited in a supersonic stream ground tests. Excessive heating leads to thermal choking: a normal shock and a consequent subsonic flow region is established in the combustor. In addition to a reduction in the performance, this can lead to increased structural and thermal loads and eventually lead to failure. The normal shock can also propagate upstream in the combustion chamber, and eventually interact with the isolator, creating extensive regions of boundary layer separation; moreover, the shock motion can lead to engine unstart with the entire isolator shock train moving upstream. Under these conditions the vehicle performance is compromised and extreme actions have to be taken to restart the engine. Unstart conditions can also be reached for different reasons, not directly connected to the combustion process. In particular, indications of unstart events connected to perturbations of the flow at the inlet and to thermal deformations of the structure have been observed. |
| |
| |
| Appraoch |
| QMU Framework |
| The first step in developing the QMU framework is to define one or more figures of merit (metric) to characterize successful operation of the scramjet engine. It is critical that the chosen metrics be sensitive to all the important aspects of the prediction tools (and the experiments) used in the evaluation. In the present scenario the engine-generated thrust is the key characteristic of the propulsion system, and it is an obvious choice. |
| |
| Uncertainty quantification |
| Uncertainty quantification (UQ) is used in the QMU framework in order to improve the predictive capabilities of the scramjet simulation. To that end, it is important to quantify the impact of both uncertainties and errors on the prediction of the quantity of interest (QOI). The sources of uncertainty and error in the scramjet simulation are aleatoric and epistemic uncertainty, and numerical error. |
| |
| Aleatoric or irreducible uncertainty accounts for physical variability in the parameters in the mathematical description of the problem, for example, in the initial and boundary conditions, and the geometry. The treatment of aleatoric uncertainty in a probabilistic framework in terms of probability distributions and covariance matrices is well-established. Aleatoric uncertainty propagation through computationally intensive models of complex physics resulting in highly nonlinear behavior is still a challenging task. Standard Stochastic Collocation (SC) methods, based on global polynomial Lagrangian interpolation of samples in suitable Gauss quadrature points in probability space can, in that case, prove to be unreliable and even result in unphysical predictions. The more robust Simplex Stochastic Collocation (SSC) method is, therefore, developed based on robustness concepts from the deterministic CFD community, e.g. Local Extremum Diminishing (LED), Total Variation Diminishing (TVD), and Monotonicity Preserving (MP), in a local finite element discretization of probability space using simplex elements. |
| |
| Epistemic uncertainty refers to structural uncertainty in the mathematical model form used to describe the physical system. The main sources of epistemic uncertainty in the scramjet simulation are the RANS turbulence model, and the mixing and combustion models. Epistemic uncertainty is not random in nature and can, therefore, best be represented in terms of intervals. The propagation of the intervals is most effective using an optimization approach. |
| |
| Numerical errors in the simulation can be categorized as, for example, discretization, iteration, and truncation errors. These numerical errors can be estimated using an adjoint solution approach. The main challenge is to combine the impact of these three distinct sources of uncertainty and error into one confidence metric for the prediction of the QOI of the full system performance. This forms the starting point for using QMU as a decision making tool for selecting whether to invest resources into more aleatoric sampling, epistemic model fidelity improvement, or discretization error reduction using finer meshes. |
| |
| |
| Results |
| Inferring the Flight Conditions |
| While the available HyShot II flight measurements provide a unique testbed in validation of computational models for the prediction of supersonic combustion, they cannot be ready utilized as the flight trajectory was not directly measured due to the radar tracking failure. This implies that the flight conditions, i.e., mach number, angle-of-attack, and flight altitude, are not directly available and, thus, have to be inferred from the onboard pressure, accelerometer, magnetometer and horizon sensor measurements. |
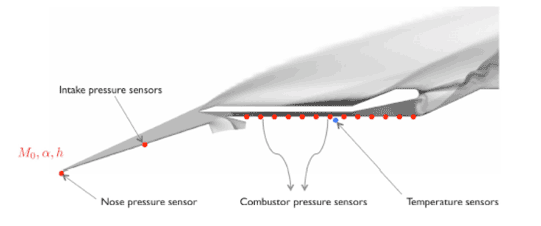 |
| We employ a two-step cross-validation approach to estimate the flight conditions and their corresponding uncertainties. In the first step, we exploit all the pressure measurements from the sensor (see above) in the unfueled combustor to infer the flight conditions using a computational Bayesian inference. The posterior distribution of the parameters obtained this way, provide an estimation of the flight condition uncertainties due the sensor measurement errors, the ill-posedness of the inference, and epistemic uncertainty in the forward computational model. In the second step, we predict the pressure measurements in the fueled combustor given the estimates of the flight condition. To this end, a probabilistic approach based on the stochastic collocation approach is used. |
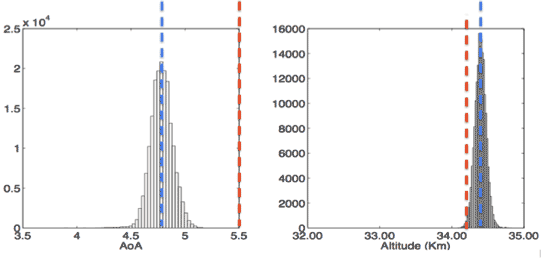 |
| The figure above shows the final estimate of the angle of attack and altitude at t=540sec after the start of the flight. The blue line represent the most likely condition, while the red line corresponds to a previous estimate based on a trajectory model of the HyShot flight. |
| |
| |
| People |
| |
| Name |
Email address |
Focus |
| Prof. Gianluca Iaccarino |
jops@stanford.edu |
Full system QMU |
| Dr. Karthik Duraisamy |
dkarthik@stanford.edu |
Adjoint reliability analysis |
| Prof. Qiqi Wang |
qiqi@mit.edu |
Adjoint reliability analysis |
| Dr. Jeroen A.S. Witteveen |
jasw@stanford.edu |
Uncertainty quantification |
|
| |
| |
[an error occurred while processing this directive]



