| Quantifying numerical discretization errors is a necessary first step in quantifying sources of uncertainty in predictive simulations. In computing the quantities of interest in the UQ and full system simulations, it is also important to control the numerical error if confidence is to be placed on the predictions. The objective of the Solution Verification effort is to provide a framework to estimate and manage the numerical error such that the simulations of the PSAAP center can be performed keeping the numerical errors within a specified tolerance. These objectives are pursued using Adjoint based techniques. This adjoint solver is also used in various other efforts within the PSAAP center including Risk analysis, Uncertainty propagation and error budgeting. |
| |
| |
| Approach |
| Adjoint based methods invoke the concept of duality (in addition to the flow solution or the primal problem, the adjoint approach involves the solution of an appropriately defined dual problem) and can be used to gain an estimate of the numerical error in computing a quantity of interest. In addition, adjoint methods can also be used to determine the local contribution to the global functional error, thus providing a reliable indicator to identify regions of the solution domain that are critical to the accuracy of the objective function in a direct manner. |
| |
| The adjoint equations can be derived in a discrete or a continuous sense. In the continuous approach, the adjoint equations are derived from the continuous flow equations and then subsequently discretized using a numerical method of choice, whereas in the discrete approach, the adjoint equations are directly derived from the discretized governing equations. These approaches offer distinct advantages in different scenarios but we have adopted to pursue the discrete adjoint approach as this enables the use of Automatic Differentiation for arbitrarily complex governing equations (thus being feasible in multiphysics applications) and is exactly consistent with the discrete governing equations (thus providing a more natural link to the discretization error). On post processing the adjoint solution, mesh adaptation indicators are derived and used in an iterative manner to keep functional errors below a tolerance level commensurate with the overall uncertainty quantification. |
| |
| The gradients computed via the adjoint solver are being used in various activities including efficient uncertainty propagation (by including gradient information at sampling points), Risk quantification (by building surrogates) and sensitivity / UQ analysis. |
| |
| |
| Results |
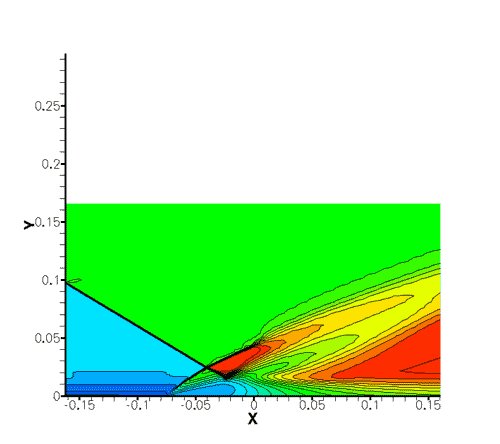 |
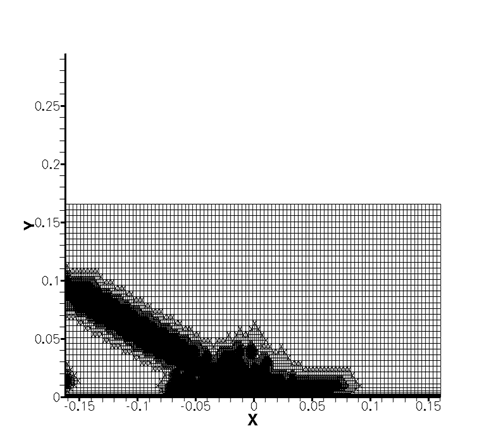
Fig. 1: Example of adjoint based mesh refinement for the case of an impiging shock on a wall. The quantity of interest is the pressure at location x=0. Using adjoints, the mesh is refined to reduce numerical errors, but only where it is required. |
| |
| |
| People |
| |
| Name |
Email address |
Focus |
| Prof. Juan Alonso |
jjalonso@stanford.edu |
All aspects |
| Prof. Karthik Duraisamy |
dkarthik@stanford.edu |
All aspects |
| Thomas Taylor |
tom.taylor@stanford.edu |
|
|

